BIOINFORMATICS WITH PARK-KLEIS

 이산형 확률분포의 종류

 : 베르누이분포, 이항분포, 이산형균등분포, 기하분포, 초기하분포, 음이항 분포, 포아송 분포 등

 각 이산형 확률분포를 살펴보도록 하겠다. 

이산형 확률변수의 적률생성함수는 다음과 같은 형태로 표현된다.

$$ M_{X}(t)=E(e^{tX})=\sum_{x=0}^{\infty}e^{tx}f(x) $$

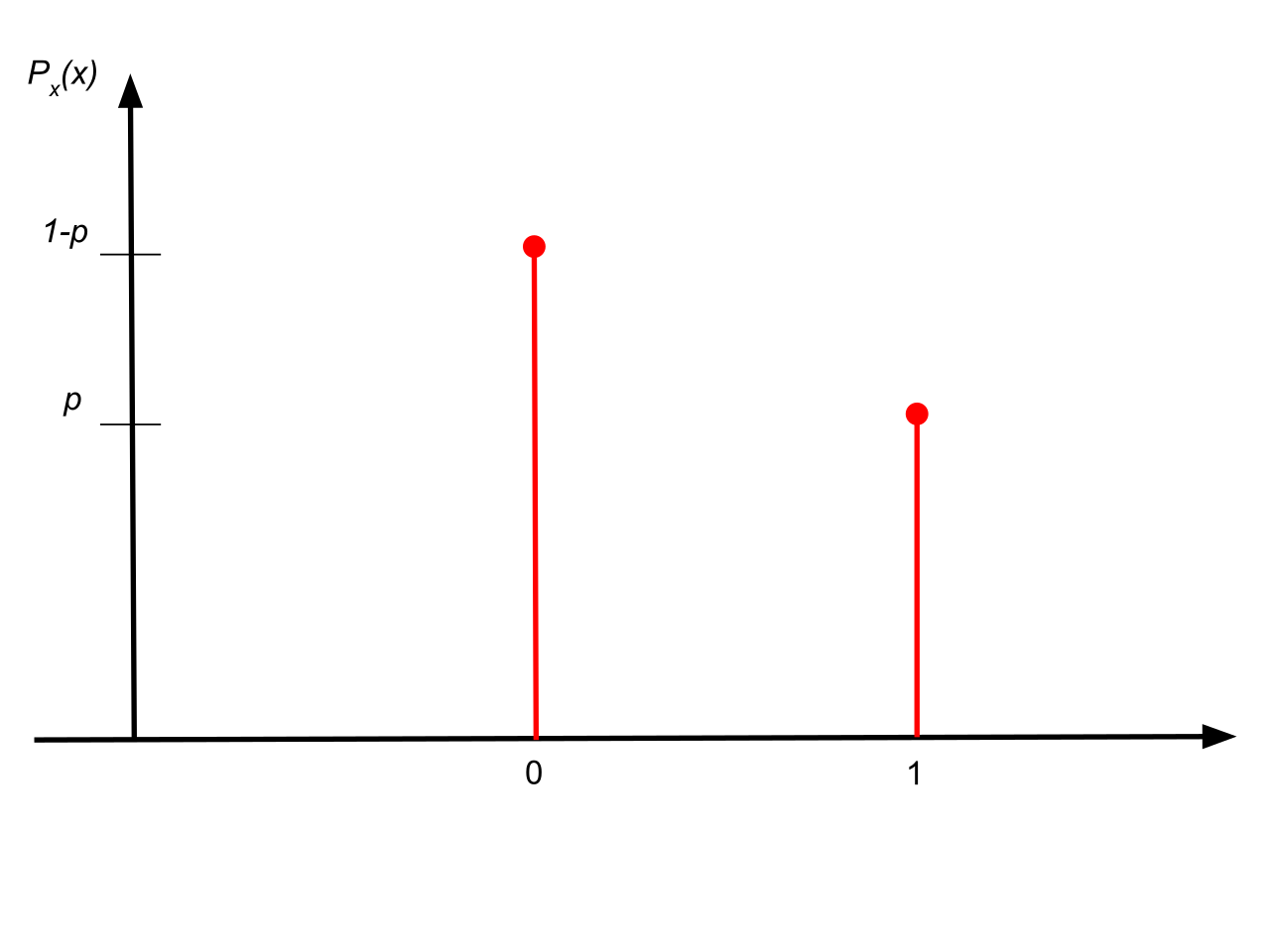
1. 베르누이 분포

베르누이 시행의 확률변수 X의 분포는 X=1의 확률에 의해 정의된다. (X=0 or 1)

P=P(X=1)=P(성공)

베르누이 시행의 확률질량함수 f(x)는

$$ f(x) = p^{x}(1-p)^{1-x}, x=0, 1 $$

베르누이 분포의 기댓값과 분산은 다음과 같다.

E(X)=p, Var(X)=p(1-p)

베르누이분포의 적률생성함수는 다음과 같다.

$$ M(t)=E(e^{tx})=(1-p)+pe^{t} $$

적률생성함수 유도 과정은 아래와 같이 진행할 수 있다.

$$ M(t)=E(e^{tX})=\sum_{x=0}^{1}e^{tx}f(x)=\sum_{x=0}^{1}e^{tx}p^{x}(1-p)^{1-x}=e^{0}p^{0}(1-p)^{1}+e^{t}p^{1}(1-p)^{0}=(1-p)+pe^{t} $$

적률생성함수를 t에 대해 1차 미분한 후 t값에 0을 대입하면 평균을 도출할 수 있다.

베르누이 분포의 적률생성함수를 1차 미분하면 

$$ M(t)=(1-p)+pe^{t}\Rightarrow M^{'}(t)=\frac{d}{dt}(1-p+pe^{t})=pe^{t} \Rightarrow M^{'}(0)=p $$

2. 이항분포

베르누이 시행을 독립적으로 n번 반복하여 시행한 경우, 성공한 총 횟수를 X라 정의하면, 이 확률변수 X는 이항분포를 따른다.

이항분포의 확률질량함수 f(x)는 다음과 같다.

$$ f(x)=\binom{n}{x}p^{x}(1-p)^{n-x}, x= 0,1,2,...,n $$

이항분포의 기댓값 E(X)=np, Var(X)=np(1-p) 이다.

이항분포 B(n, p)를 따르는 확률변수의 적률생성함수는 다음과 같다.

$$ M(t)=\sum_{x=0}^{n}e^{tx}f(x)=\sum_{x=0}^{n}e^{tx}\binom{n}{x}p^{x}(1-p)^{n-x}=[(1-p)+pe^{t}]^{n} $$

만약 n이 1이라면 베르누이분포의 적률생성함수가 된다.

3. 포아송분포

포아송분포는 이항분포에서 반복횟수인 n이 충분히 크고 성공률 p가 0에 가까울 정도로 작으면서 평균이 np=⋋일 때의 분포이다.

포아송분포는 이항분포와 밀접한 관계가 있는데, p의 값이 매우 작고 평균이 일정할 때 n이 커지면 이항분포는 포아송분포로 표현된다.

n ⇨ ∞ , p ⇨ 0 이며, np=⋋라고 가정하면 아래 식이 성립한다.

$$ \displaystyle \lim_{ n\to \infty}\binom{n}{x}p^{x}(1-p)^{n-x} $$

위 식을 풀어보면,

$$ \displaystyle \lim_{ n\to \infty}\binom{n}{x}p^{x}(1-p)^{n-x}=\displaystyle \lim_{ n\to \infty}\frac{n(n-1)\cdots (n-x+1)}{x!}(\frac{\lambda}{n})^{x}(1-\frac{\lambda}{n})^{n-x} $$

또 위의 식을 풀어보면 다음과 같다.

$$ \frac{\lambda^{x}}{x!}\displaystyle \lim_{ n\to \infty}(1-\frac{\lambda}{n})^{n}(1-\frac{\lambda}{n})^{-x}(1-\frac{1}{n})(1-\frac{2}{n})\cdots (1-\frac{x-1}{n}) $$

위 식에서 다음 성질을 만족하기 때문에

$$ \displaystyle \lim_{ n\to \infty}(1-\frac{\lambda}{n})^{n}=\displaystyle \lim_{ n\to \infty}[(1-\frac{\lambda}{n})^{\frac{n}{-\lambda}}]^{-\lambda}=e^{-\lambda} $$

다음과 같이 이항분포가 n이 매우 커지고 p값이 작을 때 포아송분포로 근사함을 표현할 수 있다.

$$ \lim_{ n\to \infty}\binom{n}{x}p^{x}(1-p)^{n-x}=\frac{\lambda^{x}e^{-\lambda}}{x!} $$

포아송분포의 확률질량함수는 다음과 같이 표현할 수 있다.

$$ f(x)=P(X=x)=\frac{\lambda^{x}e^{-\lambda}}{x!}, x=0,1,2,\cdots (\lambda>0) $$

확률질량함수를 통해 포아송분포의 적률생성함수를 아래와 같이 도출할 수 있다.

$$ M(t)=\sum_{x=0}^{\infty}e^{tx}\frac{\lambda^{x}e^{-\lambda}}{x!}=e^{-\lambda}\sum_{x=0}^{\infty}\frac{(\lambda e^{t})^{x}}{x!} $$

이를 테일러 전개를 이용하여 정리하면 

$$ M(t)=e^{-\lambda}\sum_{x=0}^{\infty}\frac{(\lambda e^{t})^{x}}{x!}=e^{\lambda(e^{t}-1)} $$ 

위 적률생성함수를 t에 대해 1차 미분한 후 t에 0을 대입하면, 포아송분포의 기댓값을 구할 수 있다.

Distribution 별 수리 통계학을 정리의 첫 번째는 Bernoulli distribution 이다.

베르누이 분포는 동전의 앞, 뒤처럼 오직 두 가지 범주만 가진 이산형 확률분포이다.

예를 들어, 시험을 봤을 때 60점 이상이면 합격, 미만이면 불합격이라 하자.

- 60점 이상 = 합격 ⇨ 이를 1이라 하고, 합격할 확률을 P(X=1) 로 표기할 수 있다.

- 60점 미만 = 불합격 ⇨ 이를 0이라 하고, 불합격할 확률을 P(X=0) 로 표기할 수 있다.

❗베르누이 분포의 확률질량함수 𝒇(𝒙)는 다음과 같다.

$$ f(x)=P(X=x)=p^{x}(1-p)^{1-x}, x=0,1 $$

❗베르누이 분포를 따르는 확률변수의 기댓값 E(X)=p, 분산 Var(X)=p(1-p) 이다.

❗베르누이 분포의 적률생성함수는 다음과 같다.

$$ M(t)=E(e^{tX})=(1-p)+pe^{t} $$

위 적률생성함수를 증명해보자.

베르누이분포는 이산형 확률분포이므로, 베르누이분포를 따르는 확률변수 X의 적률생성함수는 다음과 같이 정의된다.

$$ M_{X}(t)=E(e^{tX})=\sum_{x=0}^{\infty}e^{tx}f(x)=\sum_{x=0}^{\infty}e^{tx}p^{x}(1-p)^{1-x} $$

𝒙는 오로지 0과 1이므로, 이를 위에 대입하면,

$$ M_{X}(t)=\sum_{x=0}^{\infty}e^{tx}p^{x}(1-p)^{1-x}=e^{0}p^{0}(1-p)^{1} + e^{t}p^{1}(1-p)^{0}=(1-p)+pe^{t} $$

따라서 베르누이분포의 적률생성함수는 다음과 같다.

$$ M_{X}(t)=(1-p)+pe^{t} $$

✏이번에는 베르누이분포의 가능도함수, 로그가능도함수를 살펴본 후 최대가능도추정량을 구해보도록 하겠다.

❗먼저 가능도함수를 구해보자.

$$ L(\theta)=\prod_{i=1}^{n}f(x_{i}|\theta)=\prod_{i=1}^{n}p^{x_{i}}(1-p)^{1-x_{i}}=p^{\sum_{i=1}^{n}x_{i}}(1-p)^{n-\sum_{i=1}^{n}x_{i}} $$

❗이 가능도함수에 로그를 취한 함수를 로그가능도함수라 하는데, 이를 구해보자.

가능도함수에 로그를 취하면 다음과 같고,

$$ logL(\theta)=log(p^{\sum_{i=1}^{n}x_{i}}(1-p)^{n-\sum_{i=1}^{n}x_{i}}) $$

이는 다음과 같이 풀이할 수 있다.

$$ logL(\theta)=\sum_{i=1}^{n}x_{i} logp + (n-\sum_{i=1}^{n}x_{i}) log(1-p) $$

가능도함수 L(θ|𝑥)는 확률표본에서 얻을 수 있는 모수의 모든 정보를 가지고 있다.

따라서 이를 바탕으로 모수에 대한 가능성이 가장 높은 통계량을 찾는 것을 고려할 수 있다.

모수 θ에 대해 가능도함수 L(θ|𝑥)를 최대로 하는 통계량을 최대가능도추정량이라 한다.

❗최대가능도추정량은 로그가능도함수에 대해 미분하여 0을 만족하는 hat(θ)이다.

위에서 로그가능도 함수를 모수인 p에 대해 미분하여 0으로 놓으면 다음과 같다.

$$ \frac{d}{dp}logL(p)=\frac{\sum_{i=1}^{n}x_{i}}{p} - \frac{n-\sum_{i=1}^{n}x_{i}}{1-p}=0 $$

이를 풀면

$$ \frac{(1-p)\sum_{i=1}^{n}x_{i}-p(n-\sum_{i=1}^{n}x_{i})}{p(1-p)}=\frac{\sum_{i=1}^{n}x_{i}-np}{p(1-p)}= 0 $$

가 되고, 이를 만족하기 위해서는

$$ \sum_{i=1}^{n}x_{i}=np $$ 

이므로, 따라서 최대가능도추정량은

$$ \widehat{p}= \frac{1}{n} \sum_{i=1}^{n}x_{i} $$

한 가지 더, 로그가능도함수를 두 번 미분하면 0보다 작은 값이 되므로 hat(p)에서 가능도함수의 최댓값을 얻을 수 있다.