BIOINFORMATICS WITH PARK-KLEIS

 이산형 확률분포의 종류

 : 베르누이분포, 이항분포, 이산형균등분포, 기하분포, 초기하분포, 음이항 분포, 포아송 분포 등

 각 이산형 확률분포를 살펴보도록 하겠다. 

이산형 확률변수의 적률생성함수는 다음과 같은 형태로 표현된다.

$$ M_{X}(t)=E(e^{tX})=\sum_{x=0}^{\infty}e^{tx}f(x) $$

1. 베르누이 분포

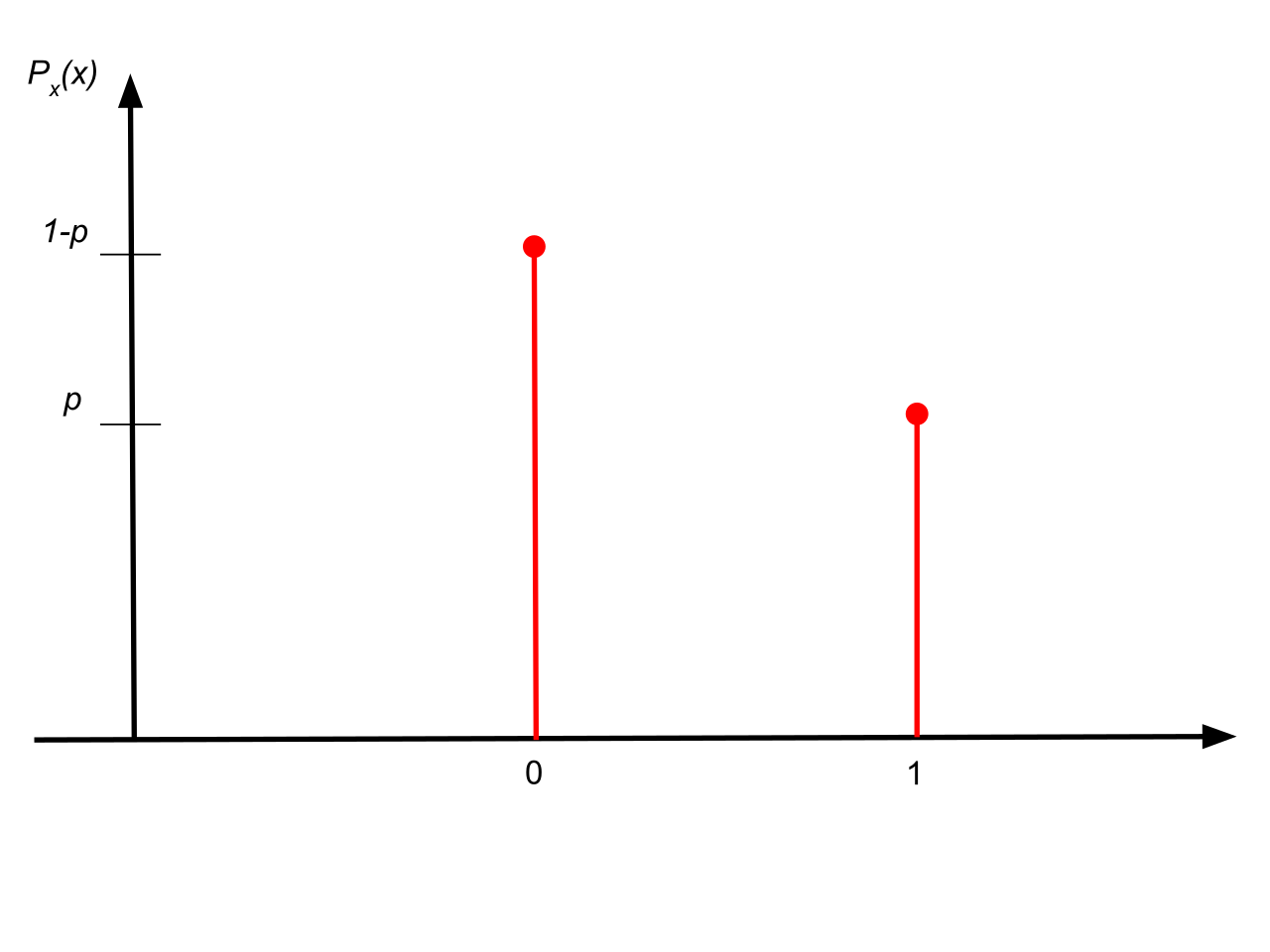
베르누이 시행의 확률변수 X의 분포는 X=1의 확률에 의해 정의된다. (X=0 or 1)

P=P(X=1)=P(성공)

베르누이 시행의 확률질량함수 f(x)는

$$ f(x) = p^{x}(1-p)^{1-x}, x=0, 1 $$

베르누이 분포의 기댓값과 분산은 다음과 같다.

E(X)=p, Var(X)=p(1-p)

베르누이분포의 적률생성함수는 다음과 같다.

$$ M(t)=E(e^{tx})=(1-p)+pe^{t} $$

적률생성함수 유도 과정은 아래와 같이 진행할 수 있다.

$$ M(t)=E(e^{tX})=\sum_{x=0}^{1}e^{tx}f(x)=\sum_{x=0}^{1}e^{tx}p^{x}(1-p)^{1-x}=e^{0}p^{0}(1-p)^{1}+e^{t}p^{1}(1-p)^{0}=(1-p)+pe^{t} $$

적률생성함수를 t에 대해 1차 미분한 후 t값에 0을 대입하면 평균을 도출할 수 있다.

베르누이 분포의 적률생성함수를 1차 미분하면 

$$ M(t)=(1-p)+pe^{t}\Rightarrow M^{'}(t)=\frac{d}{dt}(1-p+pe^{t})=pe^{t} \Rightarrow M^{'}(0)=p $$

2. 이항분포

베르누이 시행을 독립적으로 n번 반복하여 시행한 경우, 성공한 총 횟수를 X라 정의하면, 이 확률변수 X는 이항분포를 따른다.

이항분포의 확률질량함수 f(x)는 다음과 같다.

$$ f(x)=\binom{n}{x}p^{x}(1-p)^{n-x}, x= 0,1,2,...,n $$

이항분포의 기댓값 E(X)=np, Var(X)=np(1-p) 이다.

이항분포 B(n, p)를 따르는 확률변수의 적률생성함수는 다음과 같다.

$$ M(t)=\sum_{x=0}^{n}e^{tx}f(x)=\sum_{x=0}^{n}e^{tx}\binom{n}{x}p^{x}(1-p)^{n-x}=[(1-p)+pe^{t}]^{n} $$

만약 n이 1이라면 베르누이분포의 적률생성함수가 된다.

3. 포아송분포

포아송분포는 이항분포에서 반복횟수인 n이 충분히 크고 성공률 p가 0에 가까울 정도로 작으면서 평균이 np=⋋일 때의 분포이다.

포아송분포는 이항분포와 밀접한 관계가 있는데, p의 값이 매우 작고 평균이 일정할 때 n이 커지면 이항분포는 포아송분포로 표현된다.

n ⇨ ∞ , p ⇨ 0 이며, np=⋋라고 가정하면 아래 식이 성립한다.

$$ \displaystyle \lim_{ n\to \infty}\binom{n}{x}p^{x}(1-p)^{n-x} $$

위 식을 풀어보면,

$$ \displaystyle \lim_{ n\to \infty}\binom{n}{x}p^{x}(1-p)^{n-x}=\displaystyle \lim_{ n\to \infty}\frac{n(n-1)\cdots (n-x+1)}{x!}(\frac{\lambda}{n})^{x}(1-\frac{\lambda}{n})^{n-x} $$

또 위의 식을 풀어보면 다음과 같다.

$$ \frac{\lambda^{x}}{x!}\displaystyle \lim_{ n\to \infty}(1-\frac{\lambda}{n})^{n}(1-\frac{\lambda}{n})^{-x}(1-\frac{1}{n})(1-\frac{2}{n})\cdots (1-\frac{x-1}{n}) $$

위 식에서 다음 성질을 만족하기 때문에

$$ \displaystyle \lim_{ n\to \infty}(1-\frac{\lambda}{n})^{n}=\displaystyle \lim_{ n\to \infty}[(1-\frac{\lambda}{n})^{\frac{n}{-\lambda}}]^{-\lambda}=e^{-\lambda} $$

다음과 같이 이항분포가 n이 매우 커지고 p값이 작을 때 포아송분포로 근사함을 표현할 수 있다.

$$ \lim_{ n\to \infty}\binom{n}{x}p^{x}(1-p)^{n-x}=\frac{\lambda^{x}e^{-\lambda}}{x!} $$

포아송분포의 확률질량함수는 다음과 같이 표현할 수 있다.

$$ f(x)=P(X=x)=\frac{\lambda^{x}e^{-\lambda}}{x!}, x=0,1,2,\cdots (\lambda>0) $$

확률질량함수를 통해 포아송분포의 적률생성함수를 아래와 같이 도출할 수 있다.

$$ M(t)=\sum_{x=0}^{\infty}e^{tx}\frac{\lambda^{x}e^{-\lambda}}{x!}=e^{-\lambda}\sum_{x=0}^{\infty}\frac{(\lambda e^{t})^{x}}{x!} $$

이를 테일러 전개를 이용하여 정리하면 

$$ M(t)=e^{-\lambda}\sum_{x=0}^{\infty}\frac{(\lambda e^{t})^{x}}{x!}=e^{\lambda(e^{t}-1)} $$ 

위 적률생성함수를 t에 대해 1차 미분한 후 t에 0을 대입하면, 포아송분포의 기댓값을 구할 수 있다.

처음 통계를 접할 때 이해하기 어려웠던 것이 모평균, 표본평균, 표본평균의 평균 개념이었다.

지금 생각해보면 저 단어의 의미를 잘 살펴보기만 하면 크게 어렵지 않은 개념인데,

처음엔 다 어렵듯이 표본평균과 표본평균의 평균이라는 개념이 잘 이해가 가지 않았다. 

표본평균은 표본들의 평균이고, 왜 구하는지 이해가 갔는데

표본평균의 평균은 도대체 왜 구해야하는지 잘 이해가 가지 않았다.

표본평균은 중요한 성질들이 있다. 모집단을 임의로 정한 후, 시뮬레이션을 해보면,

1) 표본평균의 전체평균은 모평균과 같다.

2) 표본평균은 모평균의 비편향추정량(unbiased estimator)이다.

3) 표본평균은 모평균과 서로 다르지만 표본평균의 도수들은 모평균 주위에 많이 몰려 있다.

4) 모든 가능한 표본평균의 분포는 모평균을 중심으로 대칭형이다.

모집단이 매우 크다면, 모든 가능한 표본을 찾아 표본평균의 분포를 찾는 것은 불가능하지만

위 성질들은 ①모집단이 크거나 ②다른 분포형태를 가져도, 변함이 없다.

모평균 µ와 모분산 σ² 를 갖는 모집단에서 추출한 랜덤표본을 X₁ , X₂ , ... , X_n 이라 하면, 이들의 표본평균은 다음과 같다.

$$ \overline{X} = \frac{1}{n}(X_{1}+X_{2}+...+X_{n}) $$ 

$$ E(\overline{X})=\mu, Var(\overline{X})=\frac{\sigma^{2}}{n} $$

모집단이 무한모집단이고 표본크기가 충분히 크면 모집단이 어떠한 분포이더라도 표본평균의 분포는 근사적으로 정규분포를 따른다. 이를 중심극한정리(central limit theorem)라 한다. 

중심극한정리에 따르면 모집단의 분포와 관계없이 표본크기가 충분이 크면 표본평균은 정규분포를 따른다. 

$$ \overline{X} \sim N(\mu, \frac{\sigma^{2}}{n}) $$

따라서 이항확률변수(binomial)의 분포 역시, 표본크기 n이 충분히 큰 경우 근사적으로 정규분포를 따르게 된다.

이항분포 B(n, p)를 따르는 확률변수 X는 n이 충분히 클 때, 근사적으로 평균이 np, 분산이 np(1-p)인 정규분포 N(np, np(1-p))를 따른다.

$$ \frac{X-np}{\sqrt{np(1-p)}} \sim N(0, 1) $$

Binomial distribution

성공확률을 p라고 할 때, '성공'이면 1, '실패'면 0으로 대응시키는 확률변수를 베르누이 확률변수라 한다. 베르누이 확률변수 X의 확률분포는 다음과 같이 정의할 수 있다.

따라서, X=0인 경우에는 P(X=0) = (1-p)이고, X=1인 경우에는 P(X=1) = p가 된다.

베르누이분포의 평균은 E(X)=p, Var(X)=p(1-p) 이다.

이처럼 동일한 성공확률을 가진 베르누이 시행을 독립적으로 반복하여 시행할 때,

성공확률이 p인 베르누이 시행을 n번 독립적으로 반복 시행할 때, '성공횟수(=X)'가 x일 확률은 다음과 같이 표시할 수 있다.

이항분포의 평균은 E(X)=np, 분산은 Var(X)=np(1-p) 이다.

증명은 https://proofwiki.org/wiki/Variance_of_Binomial_Distribution 참고하면 된다.

여기에서 n, p를 이항분포의 모수(parameter)라 한다.

만약 n=1이라면, 이항분포 B(n, p)는 '1(성공)'의 확률이 p인 베르누이분포이다.

참고로 모수는 모집단의 특성값으로, 평균, 분산, 성공확률 등을 예시로 들 수 있다.

Distribution 별 수리 통계학을 정리의 첫 번째는 Bernoulli distribution 이다.

베르누이 분포는 동전의 앞, 뒤처럼 오직 두 가지 범주만 가진 이산형 확률분포이다.

예를 들어, 시험을 봤을 때 60점 이상이면 합격, 미만이면 불합격이라 하자.

- 60점 이상 = 합격 ⇨ 이를 1이라 하고, 합격할 확률을 P(X=1) 로 표기할 수 있다.

- 60점 미만 = 불합격 ⇨ 이를 0이라 하고, 불합격할 확률을 P(X=0) 로 표기할 수 있다.

❗베르누이 분포의 확률질량함수 𝒇(𝒙)는 다음과 같다.

$$ f(x)=P(X=x)=p^{x}(1-p)^{1-x}, x=0,1 $$

❗베르누이 분포를 따르는 확률변수의 기댓값 E(X)=p, 분산 Var(X)=p(1-p) 이다.

❗베르누이 분포의 적률생성함수는 다음과 같다.

$$ M(t)=E(e^{tX})=(1-p)+pe^{t} $$

위 적률생성함수를 증명해보자.

베르누이분포는 이산형 확률분포이므로, 베르누이분포를 따르는 확률변수 X의 적률생성함수는 다음과 같이 정의된다.

$$ M_{X}(t)=E(e^{tX})=\sum_{x=0}^{\infty}e^{tx}f(x)=\sum_{x=0}^{\infty}e^{tx}p^{x}(1-p)^{1-x} $$

𝒙는 오로지 0과 1이므로, 이를 위에 대입하면,

$$ M_{X}(t)=\sum_{x=0}^{\infty}e^{tx}p^{x}(1-p)^{1-x}=e^{0}p^{0}(1-p)^{1} + e^{t}p^{1}(1-p)^{0}=(1-p)+pe^{t} $$

따라서 베르누이분포의 적률생성함수는 다음과 같다.

$$ M_{X}(t)=(1-p)+pe^{t} $$

✏이번에는 베르누이분포의 가능도함수, 로그가능도함수를 살펴본 후 최대가능도추정량을 구해보도록 하겠다.

❗먼저 가능도함수를 구해보자.

$$ L(\theta)=\prod_{i=1}^{n}f(x_{i}|\theta)=\prod_{i=1}^{n}p^{x_{i}}(1-p)^{1-x_{i}}=p^{\sum_{i=1}^{n}x_{i}}(1-p)^{n-\sum_{i=1}^{n}x_{i}} $$

❗이 가능도함수에 로그를 취한 함수를 로그가능도함수라 하는데, 이를 구해보자.

가능도함수에 로그를 취하면 다음과 같고,

$$ logL(\theta)=log(p^{\sum_{i=1}^{n}x_{i}}(1-p)^{n-\sum_{i=1}^{n}x_{i}}) $$

이는 다음과 같이 풀이할 수 있다.

$$ logL(\theta)=\sum_{i=1}^{n}x_{i} logp + (n-\sum_{i=1}^{n}x_{i}) log(1-p) $$

가능도함수 L(θ|𝑥)는 확률표본에서 얻을 수 있는 모수의 모든 정보를 가지고 있다.

따라서 이를 바탕으로 모수에 대한 가능성이 가장 높은 통계량을 찾는 것을 고려할 수 있다.

모수 θ에 대해 가능도함수 L(θ|𝑥)를 최대로 하는 통계량을 최대가능도추정량이라 한다.

❗최대가능도추정량은 로그가능도함수에 대해 미분하여 0을 만족하는 hat(θ)이다.

위에서 로그가능도 함수를 모수인 p에 대해 미분하여 0으로 놓으면 다음과 같다.

$$ \frac{d}{dp}logL(p)=\frac{\sum_{i=1}^{n}x_{i}}{p} - \frac{n-\sum_{i=1}^{n}x_{i}}{1-p}=0 $$

이를 풀면

$$ \frac{(1-p)\sum_{i=1}^{n}x_{i}-p(n-\sum_{i=1}^{n}x_{i})}{p(1-p)}=\frac{\sum_{i=1}^{n}x_{i}-np}{p(1-p)}= 0 $$

가 되고, 이를 만족하기 위해서는

$$ \sum_{i=1}^{n}x_{i}=np $$ 

이므로, 따라서 최대가능도추정량은

$$ \widehat{p}= \frac{1}{n} \sum_{i=1}^{n}x_{i} $$

한 가지 더, 로그가능도함수를 두 번 미분하면 0보다 작은 값이 되므로 hat(p)에서 가능도함수의 최댓값을 얻을 수 있다.