BIOINFORMATICS WITH PARK-KLEIS

 Regression model을 만들다 보면, 독립변수로 명목형 변수를 사용할 때가 많다. 지역이나 성별, biomaker유/무 등이 대표적으로 많이 사용되는 명목형 변수로, 특히 medical 저널에서는 성별을 covariate으로 취급하여 성별에 따른 종속변수의 차이를 보고자 할 때가 많다.

명목형 변수들은 Dummy Variable로 바꾸어서 regression model을 만드는데, one hot 인코딩 방식으로 더미 변수들을 만든다.

예를 들면, 

❕ male=0, female=1

❕ Biomarker유=1, Biomarker무=0

이런식으로 만든다.

이와 같은 binary 데이터들은 더미 변수로 만드는 것도 쉽고 큰 문제가 되지 않는다.

one-hot encoding의 이유는, 0과 1 대신 빨간색, 녹색, 파란색을 1,2,3 으로 코딩해버리면, 적합한 모델은 숫자가 더 큰 3을 빨간색보다 더 중요한 인자로 생각하게 되기 때문이다. 학력처럼 순서형이면 각 숫자에 의미가 있지만 여러 컬러처럼 단순 명목형일 때에는 one-hot 인코딩을 해야한다. 

(단, 컬러가 연함 - 진함과 같이 순서형이라면 굳이 one-hot 인코딩을 안해도 된다.)

one-hot encoding의 예시는 아래 세 가지 카테고리로 보면 더 명확하게 이해가 된다.

(image출처: https://towardsdatascience.com/encoding-categorical-variables-one-hot-vs-dummy-encoding-6d5b9c46e2db)

그럼 binary 말고 여러 카테고리가 있는 변수의 경우는 어떤 식으로 더미 변수를 만들까?

Regression 모델을 만들 때에는 k개의 카테고리가 있다면, k-1개의 더미변수를 생성하게 된다. 위 그림에서 Blue일 때, d1, d2, d3 모두 0으로 코딩해도 Red, Green과 차이가 있으므로, d1과 d2만 만들어도 무방하다는 의미이다. 즉, d1과 d2가 0일 때, Blue가 되는 것이다.

이것도 예를 들어 보면 쉽게 이해가 되는데,

명목형 변수 중에 지역이나 부서 같은 여러 카테고리가 있는 변수를 생각해보자.

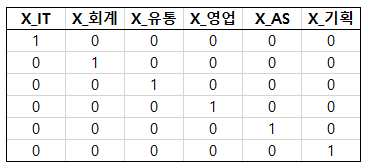
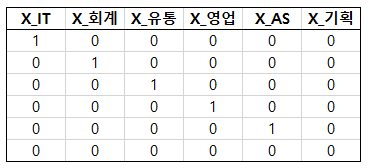
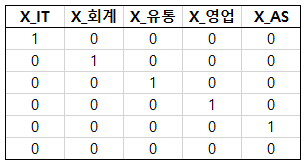
IT부서, 회계부서, 유통부서, 영업부서, AS부서, 기획부서 이렇게 6개의 부서가 있다고 하자.

그럼 총 6개의 카테고리를 다음과 같이 one-hot encoding 할 수 있다.

 회귀 모형 (Regression model) 을 적합하고 모형 진단을 할 때 여러 검정이 필요한데, 그 중에서도 먼저 적합도 검정에 대해서 살펴보고자 한다.

관심 있는 모형을 M 이라 하고, 이 모형이 잘 적합되었는지 검정을 해보자.

✅적합도 검정 (Goodness of fit test)이란? 

-포화모형에는 포함되어 있지만 간단한 모형에는 포함되지 않는 모든 모수가 0인지 검정하는 것

✔ 귀무가설: 간단한 모형 (현재 고려하고 있는 모형 = M)

✔ 대립가설: 포화모형 (가장 복잡한 모형)

유의확률이 클수록 귀무가설을 기각하지 못하기 때문에 간단한 모형을 선택하게 된다. 즉, 유의확률이 크다면 간단한 모형이 복잡모형과의 설명력에서 차이가 없으므로 간단한 모형을 사용하면 된다.

범주형 변수 4개(binary)가 있다면 모수가 4개.

✅적합도와 이탈도

GLM에서 적합도 검정을 위한 가능도비 통계량

1. 이탈도(Deviance) = -2[Lm-Ls] 

    Ls:포화모형의 이탈도, Lm: 간단모델의 이탈도

값이 클수록 포화모형과 비교했을 때 축소모형의 설명력이 좋지 못하다는 해석을 내릴 수 있음. P-value가 작을수록 적합결여에 대한 강한 증거가 된다.

2. 대표본의 경우 근사적으로 카이제곱 분포를 따름.

예측변수가 모두 범주형 변수인 경우, 전체 Data는 분할표의 도수로 요약할 수 있다.

잔차를 이용해 적합도를 살펴볼 수 있다.

LM = 모형 M 에서 얻은 로그 가능도함수의 최댓값

LS = 가능한 모형 중에서 가장 복잡한 모형에서의 로그 가능도함수의 최댓값

가장 복잡한 모형을 포화모형 saturated model 이라고 하고, 이 모형은 각 관측값에 대해 모수를 가지므로 완벽하게 자료를 적합시킨다.

포화모형은 모수들을 더 많이 포함하기 때문에 포화모형 하에서 구한 로그가능도함수의 최댓값 LS는 더 단순한 모형인 M 에서 구한 로그가능도함수의 최댓값 LM 보다 큰 값을 갖는다.

GLM의 이탈도 통계량은 다음과 같이 정의할 수 있다.

$$ 2[L_{S}-L_{M}]\sim \chi^{2},\:\;  L_{S} > L_{M} $$

이탈도 통계량의 귀무가설

- 포화모형의 모수들 중, 모형 M에 포함되지 않은 모수들이 모두 0이다.

 = 모형 M 이 포화모형보다 더 괜찮은 모형이다.

 = 모형 M 이 잘 적합되었다.

따라서 이 경우에는 P-value 값이 높을수록 관심 있는 모형 M 의 적합성이 좋다.

 GLM 적합 후에 여러 가지를 검정해야 하는데, 이번에는 설명변수에 대한 검정을 살펴보도록 하겠다.

표본이 큰 경우에 GLM의 ML 추정량들은 근사적으로 정규분포를 따른다.

설명변수가 한 개인 GLM을 생각해보자.

(1) 왈드검정 Wald

귀무가설 β=0 을 검정하기 위한 왈드 검정통계량은 다음과 같다.

$$ z=\hat{\beta}/SE $$

귀무가설 하에서 z는 근사적으로 표준정규분포를 따른다.

$$ z^{2} \sim \chi^{2} (df=1) $$

이항모수 𝛑에 대하여 SE는 다음과 같다.

$$ SE=\sqrt{\hat{\pi}(1-\hat{\pi})/n} $$

(2) 가능도비 검정 Likelihood ratio

l 0 = 귀무가설 하에서의 가능도함수의 최댓값

l 1 = 완전모형 하에서의 가능도함수의 최댓값

$$ 2log(l_{1}/l_{0})=2[log(l_{1})-log(l_{0})]=2(L_{1}-L_{0}) $$

L0 = 귀무가설 하에서의 로그 가능도함수의 최댓값

L1 = 완전모형 하에서의 로그 가능도 함수의 최댓값

(로그변환과 두 배를 하면 대략적으로 카이제곱 표본분포를 따르게 됨)

귀무가설 β=0 하에서 2(L1-L0) 이 검정통계량은 근사적으로 자유도가 1인 카이제곱분포를 따른다.

가능도비 검정은 일반적으로 왈드검정보다 statistical power가 더 높다고 평가 받는다.

(3) 스코어 검정 score test

왈드 검정과 달리 추정된 표준오차값이 아닌, 귀무가설이 참일 때 타당한 표준오차값(SE0)을 이용한다.

왈드 검정에서 SE는 다음과 같다.

$$ SE=\sqrt{\hat{\pi}(1-\hat{\pi})/n} $$

z검정에서 사용하는 표준오차 즉, 스코어 검정에서 SE0는 다음과 같다.

$$ SE_{0}=\sqrt{\pi_{0}(1-\pi_{0})/n} $$

 모든 GLM은 세 개의 성분이 있다.

(1) 랜덤성분 random component

 - 반응변수 Y를 정의하며, 반응변수 Y에 대한 확률분포를 가정한다.

(2) 선형예측식 linear predictor

- 설명변수(=독립변수)들을 명시함. 변수들이 선형식의 우변에 다음과 같은 형태로, 예측변수들의 선형식으로 들어가는 것을 의미한다.

$$ \alpha+\beta_{1}x_{1}+\cdots +\beta_{n}x_{n} $$

모형에 대한 통계적 추론은 독립변수들의 관측값들을 고정된 값으로 간주한 조건부 추론을 하게 됨.

(3) 연결함수 link function

- Y에 대한 확률분포의 기댓값 E(Y)는 설명변수(=독립변수)들의 값에 따라 달라진다.

$$ g(\mu)=\alpha +\beta_{1}x_{1}+\cdots +\beta_{n}x_{n} $$

여기에서 연결함수는 "g" 로 랜덤성분과 설명변수들의 선형예측식을 연결하는 함수다.

✔ 연결함수의 가장 간단한 형태는

$$ g(\mu)=\mu $$

 이 연결함수는 평균자체를 모형화하므로 항등연결함수 identity link function 라고 한다.

$$ \mu=\alpha +\beta_{1}x_{1}+\cdots +\beta_{n}x_{n} $$

이 형태는 연속형(=양적) 반응변수에 대한 보통의 회귀모형 형태다. 일반적인 선형회귀(linear regression)이라 생각하면 된다.

❗다른 연결함수를 사용하면 µ를 설명변수의 비선형식으로 표현이 가능하다.

✔ 예를 들면 아래 식은 평균의 로그 변환된 값을 모형화한 것이다.

$$ g(\mu)=log(\mu) $$ 

로그함수는 양수에 대해서 정의된다.

로그 연결함수는 µ 가 도수를 나타내는 자료와 같이 양의 값을 가질 때 적절히 사용가능하다.

아래 식은 로그선형모형이라 부른다.

$$ log(\mu)=\alpha +\beta_{1}x_{1}+\cdots +\beta_{n}x_{n}$$

❗아래 연결함수는 오즈의 로그값을 모형화한다.

$$ g(\mu)=log(\frac{\mu}{1-\mu}) $$

이 연결함수는 로짓함수 Logit Link 라고 부른다. 이 연결함수는 µ 가 확률과 같이 0과 1사이에 있을 때 적절히 사용 가능하다.

로짓함수를 이용한 GLM을 로지스틱 회귀모형 logistic regression model 이라고 한다.

 앞선 글에서는 이항자료를 관측값으로 갖는 경우에 모형을 어떻게 적합할 것인가를 살펴보았다.  그럼 Counts 도수를 관측값으로 갖는 경우에는 어떻게 적합할까?

📋도수를 관측값으로 갖는 범주형 반응변수들은 예를 들어 ①디바이스 개수 ②실리콘 기판의 결함수 등이 있다.

도수자료를 가질 때 some GLM은 랜덤성분에 대해 포아송 분포 Poisson distribution을 가정한다.

❗포아송 확률은 다음 식과 같다.

$$ p(y)=\frac{e^{-\mu} \mu^{y}}{y!} , y=0,1,2, \cdots $$

포아송 분포를 따르는 데이터는 모수가 한 개다. 그 모수는 바로 μ

E(Y) = Var(Y) = μ

포아송의 평균을 모형화할 때에는 로그변환된 평균을 사용하는 것이 일반적이다.

GLM에는 세 가지 성분이 있다고 했는데, 도수자료를 가지는 GLM에서의 세 가지 성분에 대해 살펴보자.

✔ 랜덤성분: 포아송 분포

✔ 자연모수: 로그 평균

✔ 연결함수: log(μ)

포아송 로그 선형모형의 함수 그림은 아래와 같다.

하나의 설명변수 x에 대하여 포아송 로그 선형모형은 다음과 같다.

$$ log\mu=\alpha+\beta x $$

따라서 위 모형에서 평균 μ를 계산하면 다음과 같다.

$$ \mu=exp(\alpha+\beta x)=e^{\alpha}e^{\beta x}=e^{\alpha}(e^{\beta})^{x} $$

위 모형의 의미는 x가 한 단위 증가하면 μ가 exp(β)배 만큼 커진다는 뜻이다.

 회귀모형을 적합할 때 적합하고자 하는 모형의 반응변수가 Binary data라면 어떻게 모형을 만들어야 할까?

반응변수가 두 가지의 범주를 갖고 있는 경우가 참 많다.

예를 들면..

(예, 아니오) (성공, 실패) (양성, 음성)

이항반응변수를 Y라 표시하고, 성공을 1, 실패를 0이라 나타내면,

반응변수 Y의 분포는 성공에 대한 확률 P(Y=1)=π 와 실패에 대한 확률 P(Y=0)=(1-π)로 표현할 수 있다.

이 분포의 평균 E(Y)=π 이며, n개의 서로 독립적인 이항반응변수의 관측값으로부터 관측된 성공횟수는 n과 π를 모수로 갖는 이항분포를 따른다.

모수: n, π

이항반응변수를 갖는 값들을 회귀모델을 만드는 방법은 크게 두 가지이다.

1. 선형확률모형

먼저 이항반응변수를 갖는 값들을 보통선형모형을 이용해 항등연결함수를 사용해보도록 하겠다.

$$ P(Y=1)=\alpha+\beta_{1}x_{1}+\cdots +\beta_{p}x_{p} $$

이 모형은 성공확률이 설명변수에 따라 선형적으로 변하므로 Linear probability model 라고 부른다.

다른 변수가 고정되어 있을 때, x1이 한 단위 변한다면 모수 Beta1은 확률 P(Y=1)의 변화량을 의미한다.

한계점: 확률은 0과 1 사이의 값. 선형함수는 실수 전체에 걸쳐 값을 가질 수 있음. 

2. 로지스틱 회귀모형

P(Y=1) 와 x의 관계는 비선형 형태이다. x의 변화량은 P(Y=1)가 0이나 1에 가까이 있을 때, 중앙일 때보다 영향을 덜 미치게 된다. 

로지스틱 회귀함수 Logistic regression function은 다음과 같이 표현할 수 있다.

$$ P(Y=1) = \frac{exp(\alpha+\beta x)}{1+exp(\alpha+\beta x)} $$

모수 베타는 곡선이 증가하거나 감소하는 속도를 결정함.

만일 설명변수가 여러개라면 다음과 같이 표현 가능하다.

$$ log[\frac{P(Y=1)}{1-P(Y=1)}]=\alpha+\beta_{1}x_{1}+\cdots +\beta_{p}x_{p} $$

로지스틱 회귀모형은 GLM의 특별한 경우다.

랜덤성분은 이항분포

연결함수는 π=P(Y=1) 의 로짓변환인 log[π/(1-π)] = logit(π)